深度优先搜索

深度优先搜索属于图算法的一种，英文缩写为 DFS 即 Depth First Search.其过程简要来说是对每一个可能的分支路径深入到不能再深入为止，而且每个节点只能访问一次。

这种思想有时候也叫回溯法，可以使用递归的方式来实现。也可以使用非递归的方式，用栈来实现。

深度优先搜索遍历了所有可能的情况，搜索流程会形成一颗树。

示例

全排列

给定一个整数 n，将数字 1~n 排成一排，将会有很多种排列方法。 现在，请你按照字典序将所有的排列方法输出。

输入格式

共一行，包含一个整数 n。

输出格式

按字典序输出所有排列方案，每个方案占一行。 数据范围 1≤n≤7

输入样例

3

输出样例

1 2 3

1 3 2

2 1 3

2 3 1

3 1 2

3 2 1

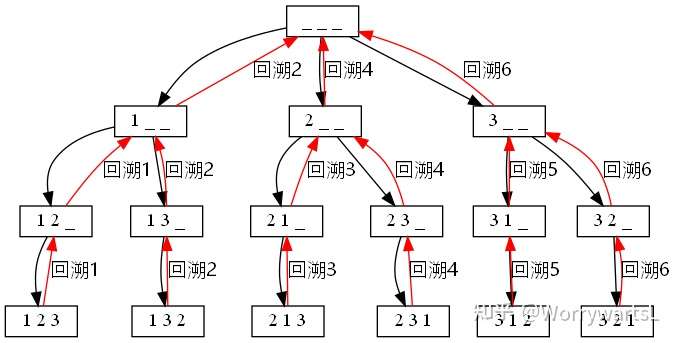
如图，首先会一路深搜到 123 然后回溯到 12_ 发现没法继续，又回溯到 1__ 然后一路深搜到 132 之后回溯、深搜……循环往复。直到最后回溯到头。回溯时一定要"恢复现场"。这种回溯和递归的实现方法，只使用了 arr 这一个空间，没有使用额外空间。

限制空间复杂度，推荐用这种方法。

def dfs(arr):
    if len(arr) == n:
        print(arr)
    for i in range(1, n + 1):
        if i not in arr:
            dfs(arr+[i])
            #回溯的写法
            #print('arr',arr) #取消注释，查看arr回溯变化过程
            #arr.append(i)
            #dfs(arr)
            #arr.pop()
            #print('arr',arr) #取消注释，查看arr回溯变化过程
n = int(input())
dfs([])

也可以使用栈的方式来实现深度优先搜索。

不限制空间复杂度，推荐用这种方法。

def dfs(node):
    for i in range(n, 0, -1): #栈先进后出，所以大的先进，最后才出。
        if i not in node:
            stack.append(node + [i])
            #print(stack) #取消注释，查看stack的变化过程

n = int(input())
root = []
stack = [root]
while stack:
    node = stack.pop()
    if len(node) == n:
        print(node)
    dfs(node)

总结

深度优先搜索也算是一种暴力枚举，不过有时候我们可以使用剪枝和记忆化的方式来减少搜索次数，从而提升效率。

适用问题：

• 限定空间

代码模板

def dfs(node):
    for child in children: #children是根据node得到的所有子节点
        if valid(child):
            stack.append(child)

stack = [root] #root是根节点
while stack:
    node = stack.pop()
    dfs(node)

练习